Question

Из пункта а в пункт в выехал автомобиль со скоростью 100км/ч через полтора часа из пункта в выехал велосипедист со скоростью 10 км/ч. встретились они в пункте с. найти расстояние от в до с. причём, если бы автомобиль ехал со скорость 120 км/ч, а велосипедист со скоростью 15 км/ч. они встретились бы на 10 км ближе к пункту а.

Answer 1

1) До момента встречи в пункте С:
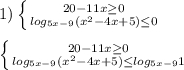
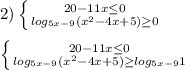
Автомобиль:
время  t ₁   ч.
скорость  100 км/ч
расстояние ( от А до С)  100t₁
Велосипедист:
время  (t₁-1.5) ч.
скорость 10 км/ч
расстояние ( от В до С)   10(t₁-1.5) км

2) Если бы участники движения ехали с другой скоростью, то они бы встретились в другом месте ,например в пункте К . И затратили на дорогу - другое время.
Автомобиль:
время  t ч.
скорость 120 км
расстояние ( от пункта А до К)  120t
Велосипед:
время (t-1.5)ч.
скорость 15 км/ч
расстояние 15(t-1.5) км

По условию задачи они бы встретились на расстоянии 10 км ближе к пункту А ( см. ≈ схему).
Значит автомобиль проехал бы на 10 км меньше , а велосипедист на 10 км больше. Приравняем расстояния.
Система уравнений:
{120t = 100t₁ -10                      |:10
{15(t-1.5) = 10(t₁-1.5) +10

{12t= 10t₁-1                              ⇒t₁= (12t+1)/10
{15t - 22.5 = 10t₁-15+10

{12t-10t₁ = -1                  |*(-1)
{15t -10t₁= -5 +22.5

{-12t +10t₁= 1
{15t -10t₁= 17.5                                 ⇒t₁= (15t-17.5)/10
Метод сложения:
-12t +10t₁+15t -10t₁= 1+17.5
3t=18.5
t= 18.5 /3 = 185/30 = 37/6
t= 6  1/6  ч.
t₁= ( 12  *  6  1/6   + 1 ) / 10 = ((2*37)/(1*1) +1 )/10 =75/10=7.5 ч.
(или t₁= (15* 6  1/6   - 17.5 ) /10  = (92.5-17.5)/10=75/10=7.5  ч.) 
t₁=7.5 ч.
Расстояние от В до С :
10 (7.5-1.5) = 10*6 = 60 км.
Проверим:
Расстояние от А до В:
1) 100 *7,5 + 10(7,5-1,5) = 750+60= 810 км
2) 120* 6  1/6   + 15  (6  1/6   - 1,5 ) = 
= (120*37) /(6*1)  +  15  ( 6 1/6  -  1  3/6 )=
=20*37     +   15/1  *  28/6  = 740 +  5*14= 740+70= 810 км

ответ : 60 км расстояние от пункта В до С.