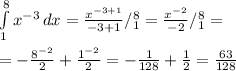
7/12
Объяснение:
Заштрихованная фигура состоит из двух криволинейных трапеций. Одна, находящаяся над осью абсцисс, ограничена графиком y = x², двумя вертикальными прямыми x = -1 и x = 0, а также самой осью Ox. Вторая, находящаяся под осью абсцисс (из-за этого ее площадь возьмем со знаком минус), ограничена графиком y = x³, теми же вертикальными прямыми и той же осью Ox.
Тогда площадь S рассматриваемой фигуры будет равна сумме двух определенных интегралов (один — от x², другой — от x³ со знаком минус), оба вычисленных на отрезке [-1; 0]:
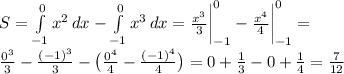

- 0,8
Объяснение:
1) Выносим cosα за скобки и затем каждый сомножитель приравниваем к 0 ("произведение равно нулю, когда один или оба сомножителя равны нулю").
4cos²α - 3sinα· cosα = 0
cosα · (4cosα - 3sinα) = 0
cosα = 0 - отбрасываем, т.к. cosα = 0, если α = π, а точка π не входит в диапазон, заданный условием задачи (π<α<3π/2).
2) Решаем вторую скобку:
(4cosα - 3sinα) = 0
а) переносим - 3sinα вправо;
4cosα = 3sinα
б) делим обе части на 4, а затем на sinα ≠ 0, получаем:
ctg α = 3/4
3) Находим sinα по формуле:
sinα = 1/(±√(1+ctg²α).
Так как α - угол 3-ей четверти, то ответ будет со знаком минус:
sinα = - 1/(√(1+9/16) = - 1/(5/4) = - 4/5 = -0,8
ответ: - 0,8