Нет точки максимума
Объяснение:
Рассмотрим функцию
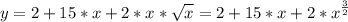
Так как в составе функции участвует квадратный корень, то область определений функции: x≥0, то есть D(y)=[0; +∞).
Чтобы найти экстремумы (локальные минимумы и максимумы) будем исследовать функцию с производной функции. Вычислим производную функции:
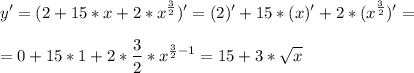
Так как 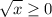 , то
, то
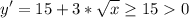
для любого x∈D(y). Это означает, что данная функция монотонно возрастает в D(y). Отсюда следует, что у функции нет точки максимума.
Так как функция монотонно возрастает в D(y), то минимальное значение в D(y)=[0; +∞) принимает при x=0: y(0)=2.
1) 2х²+7х-4<0
график парабола, ветви вверх
2х²+7х-4=0
D = 49 + 32 = 81 = 9²
x(1) = (-7+9) / 4 = 1/2
x(2) = (-7-9) / 4 = -4
/////////
-------o-------o------->x
-4 1/2
х∈(-4; 1/2)
2)3х²-5х-2>0
график парабола, ветви вверх
3х²-5х-2=0
Д = 25+24 = 49 = 7²
х(1) = (5+7)/6 = 2
х(2) = (5-7) /6 = -1/3
/////// ////////
-------о---------о------->x
-1/3 2
x∈(-∞; -1/3)∪(2; +∞)
3)-2х²+х1≥0
график парабола, ветви вниз
-2x²+x+1=0
D = 1+8 = 9 = 3²
x(1) = (-1+3) / -4 = -2/4=-1/2
x(2) = (-1-3) / -4 = -4/-4 = 1
////////
------*-------*------>x
-1/2 1
x∈[-1/2; 1]
4)-4х²+3х+1≤0
график парабола , ветви вниз
-4x²+3x+1 = 0
D = 9+16 = 25 = 5²
x(1) = (-3+5)/-8 = -1/4
x(2) = (-3-5) / -8 = 1
//////// /////////
--------*-------*------->x
-1 -1/4
x∈(-∞; -1]∪[-1/4; +∞)