V = 96 см².
Объяснение:
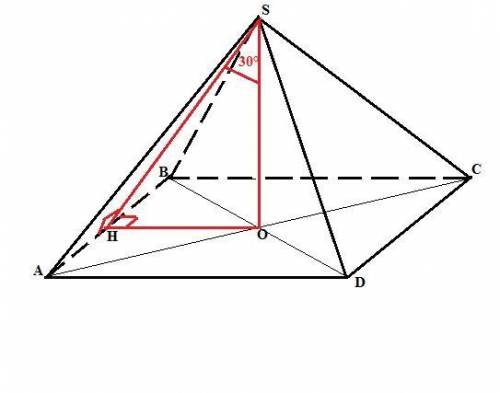
Основание правильной четырехугольной пирамиды - квадрат. Так как углом между наклонной (высота пирамиды) и плоскостью (боковая грань пирамиды) являетс угол между этой наклонной и ее проекцией на плоскость, высота боковой грани (апофема) образует с высотой пирамиды угол 30° (дано). В правильной пирамиде ее вершина проецируется в центр основания (пересечение диагоналей квадрата), расстояние от которого до боковых сторон равно половине стороны квадрата.
Рассмотрим прямоугольный треугольник SOH, образованный апофемой SH (гипотенуза), высотой пирамиды (SO) и половиной стороны основания ОН (катеты). <ОСН=30° (дано).
По Пифагору SO² = SH² - OH².
Так как катет, лежащий против угла 30° равен половине гипотенузы, то SH = 2*OH и тогда SО² = 3*ОН² = 36 см => ОН = 2√3 см.
Сторона основания равна 2*ОН = 4√3, площадь основания равна
So = (4√3)² = 48 см². Тогда
V = (1/3)*So*H = (1/3)*48*6 = 96 см²
Если квадрат наибольшей стороны равен сумме квадратов двух других сторон,то прямоугольный
Если квадрат наибольшей стороны меньше суммы квадратов двух других сторон,то остроугольный.
Если квадрат наибольшей стороны больше суммы квадратов двух других сторон, то треугольник тупоугольный
наибольшая сторона 13см
10²+7²=100+49=149- сумма квадратов двух других сторон,
13²=169 - квадрат наибольшей стороны
169>149
треугольник тупоугольный