 с прямым углом
с прямым углом  , EF — биссектриса
, EF — биссектриса  ,
,  , FG — искомый отрезок.
, FG — искомый отрезок.  .
.  — биссектриса, то
— биссектриса, то  (биссектриса
(биссектриса  делит
делит  на два равные угла).
на два равные угла). 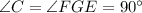 (это следует из условия: так как
(это следует из условия: так как  прямоугольный, то и
прямоугольный, то и  ; так как
; так как  — расстояние от
— расстояние от  до
до 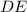 , то
, то 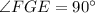 ).
).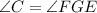 и
и 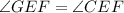 , то и третий угол первого треугольника равен третьему углу второго треугольника:
, то и третий угол первого треугольника равен третьему углу второго треугольника:  . Это следует из того факта, что сумма углов любого треугольника равна 180°. Тогда можно записать так:
. Это следует из того факта, что сумма углов любого треугольника равна 180°. Тогда можно записать так: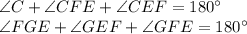
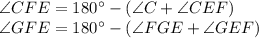
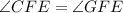 .
.  является для обоих треугольников общей.
является для обоих треугольников общей. (второй признак равенства треугольников — по стороне и двум прилежащим к ней углам (
(второй признак равенства треугольников — по стороне и двум прилежащим к ней углам ( — сторона, а
— сторона, а  — два прилежащих угла)).
— два прилежащих угла)). соответствует
соответствует  , тогда:
, тогда: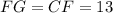
 . Смотрите второй рисунок.
. Смотрите второй рисунок.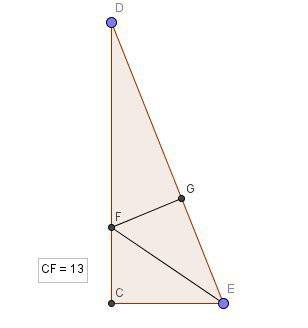
Поскольку в условии задачи не указано, лежат ли прямые в одной плоскости или нет, то они необязательно параллельны.
В планиметрии две прямые могут быть параллельными или пересекаться.
Две прямые в пространстве параллельны друг другу, пересекаются или скрещиваются.
Если две прямые лежат в одной плоскости и не пересекаются, то они - параллельны.
. В стереометрии две прямые могут не пересекаться, но в то же время не быть параллельными.
Прямые, которые не имеют общих точек и не параллельны, называются скрещивающимися.
Скрещивающиеся прямые лежат в параллельных плоскостях, но плоскость провести через них, как это можно сделать через две параллельные прямые, невозможно
Рассмотрим это на ребрах куба (см. приложение)