Следовательно ВС = 2NF – AD = 2*20 – 14 = 40 -14 = 26 cм
Объяснение:
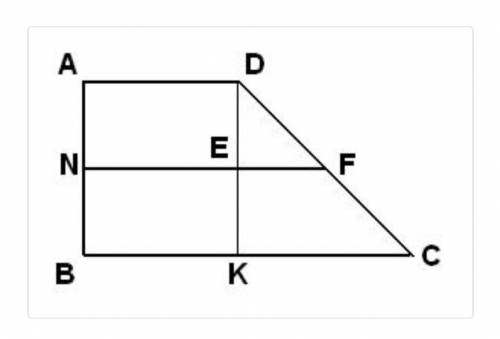
DK – перпендикуляр к ВС (см.рисунок). Так как NF - средняя линия трапеции, то AN = NB = DE = EK = AB/2 = 12/2 = 6 cм. Поскольку угол BCD = 45 градусов, то и угол NFD = 45. Тогда DE = EF = 6 см. Следовательно NE = BK = AD = NF – EF = 20 – 6 = 14 cм. В треугольнике DKC EF – его средняя линия. Посему KC = 2EF = 2*6 = 12 см. Таким образом ВС = ВК + КС. Но выше было найдено, что ВК = NE = AD = 14 см. Тогда ВС = 14 + 12 = 26 см. ВС можно было бы найти и иначе. Помните? Средняя линия трапеции равна полусумме оснований. Следовательно ВС = 2NF – AD = 2*20 – 14 = 40 -14 = 26 cм
Треугольник АВС равнобедренный, значит BD биссектриса, медиана и высота, т.е. AD = DC и ΔABD прямоугольный, а DE - его высота.
По свойству пропорциональных отрезков в прямоугольном треугольнике, квадрат катета равен произведению гипотенузы и проекции этого катета на гипотенузу:
BD² = BE · AB
AD² = AE · AB
Пусть х - коэффициент пропорциональности, тогда
АЕ = 4х, ВЕ = 9х, а АВ = 13х.
BD = √(9х · 13х) = 3х√13
AD = √(4x · 13x) = 2x√13
AC = 2AD = 4x√13.
Так как BD + AC = 14, то
3x√13 + 4x√13 = 14
7x√13 = 14
x = 2/√13 = 2√13 / 13 см
AB = BC = 13x = 2√13 см
AC = 4x√13 = 4 · 2√13/13 · √13 = 8 см
Pabc = AB + BC + AC = 2AB + AC = 2 · 2√13 + 8 = 4(√13 + 2) см
а) 1)DE= =4
=4 см
см
2)СD= =4
=4 см
см
AD= =4
=4
AB/BC=4 /4
/4 =1/
=1/
б)P=2*(4 +4
+4 )=8
)=8 +8
+8
в)S=4 *4
*4 =48
=48 см^2
см^2