смотрите чертеж.
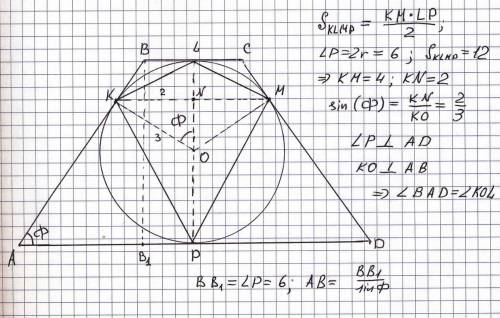
В этом 4угольнике диагонали взаимно перпендикулярны, и одна из них - диаметр окружности, то есть 6. Площадь такого 4угольника равна половине произведения диагоналей (докажите, это просто). Значит расстояние между точками касания 12*2/6 = 4. А половина - 2. Значит sin(Ф) = 2/3. Ф - половина центрального угла хорды, соединяющей точки касания. ОЧЕНЬ ЛЕГКО увидеть, что Ф - угол при большом основании трапеции (просто стороны углов перпендикулярны, см. рисунок, там отмечено). А дальше, вычисляете боковую сторону (диаметр 6 делить на sin(Ф) = 2/3), она равна средней линии (почему? - это следует из свойства описанного 4угольника - суммы боковых сторон равны сумме оснований, а боковые стороны равны между собой, значит, боковая сторона равна средней линии :)), умножаете на диаметр (то есть на высоту трапеции), задача решена. Собрав все это получаем
S = (2*r)^2/sin(Ф) = 6^2*3/2 = 54.
Ну надо же!
Я вам сразу напишу ответ. Площадь самого треугольника S = a^2*корень(3)/4;
В общем случае Sp = S*cos(Ф); Ф - угол между плоскостями. Я доказывать это не буду - либо вам это рассказывали, либо вы такие задачи не должны решать :))).
1) Sp =a^2*(корень(3)/4)*(корень(3)/2) = a^2*3/8
2) Sp = a^2*(корень(3)/4)*(корень(2)/2) = a^2*корень(6)/8;
3) Sp = a^2*корень(3)/8;
Я обычно пользуюсь этим, когда надо площадь боковой поверхности правильных пирамид считать - если угол наклона граней одинаковый, там это тоже работает. :)
Если опустить перпендикуляр ЕР из точки Е на сторону АD, то EP будет высотой как треугольника, так и трапеции.
по условию задачи ВС=AD/2
площадь треугольника S(AED) = (1/2)*AD*EP
площадь трапеции S(ABCD) = (1/2)*(AD+BC)*EP=(1/2)*(AD+AD/2)*EP=(1/2)*(1+1/2)*AD*EP = (1/2)*(3/2)*AD*EP=(3/2)*(1/2)*AD*EP = (3/2)*S(AED)
S(ABCD) = (3/2)*S(AED)
S(ABCD) = (3/2)*60 = 90
ответ: S(ABCD) = 90