Дан треугольник ABC : A(2;1),B(-1;1),C(3;2).
Найти: 1) длины всех сторон;
АВ (с) = √((Хв-Ха)²+(Ув-Уа)²) = √9 = 3.
BC (а)= √((Хc-Хв)²+(Ус-Ув)²) = √17 ≈ 4,123106.
AC (в) = √((Хc-Хa)²+(Ус-Уa)²) = √2 ≈ 1,414214.
2) внутренний угол при вершине А;
cos A= АВ²+АС²-ВС² = -0,707107.
2*АВ*АС
A = 2,3562 радиан
A = 135 градусов.
3) площадь треугольника;
S=(1/2)*|(Хв-Ха)*(Ус-Уа)-(Хс-Ха)*(Ув-Уа)| = 1,5 кв.ед.
4) уравнение прямой BN, параллельной стороне АС;
ВN || АC: Х-Хв = У-Ув
Хс-Ха Ус-Уа
1Х - 1У + 2 = 0,
у = 1х + 2.
5) уравнение медианы СD;
Основания медиан (точки пересечения медиан со сторонами).
D(ХD;УD) Ха+Хв ; Уа+Ув х у
2 2 D 0,5 1.
СD : Х-Хс = У-Ус
ХD-Хс УD-Ус
1Х - 2,5 У + 2 = 0
у = 0,4 х + 0,8.
6) уравнение высоты АЕ;
АE: Х-Ха = У-Уа
Ус-Ув Хв-Хс
4Х + 1У - 9 = 0
у = -4х + 9
7) точку пересечения медианы и высоты .
Приравняем: 0,4х + 0,8 = -4х + 9
4,4х = 8,2,
х =8,2/4,4 ≈ 1,864
у = 0,4*1,864 + 0,8 ≈ 1,546.
Построить треугольник - по координатам.
Объяснение:
удачи :)
Формула радиуса вписанной окружности
r=S/p, где S- площадь треугольника, р - его полупериемтр
р=(2•10+16):2=36:2=18
Площадь можно найти по ф.Герона, можно, найдя высоту треугольника.
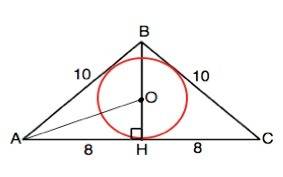
Проведем высоту ВН. Высота равнобедренного треугольника, проведенная к основанию - его медиана и биссектриса.
АН=СН=16:2=8
По т.Пифагора ВН=√(AB²-AH²)=√(100-64)=6
S=BH•AH=6•8=48
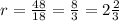
Через свойство биссектрисы решение будет другим.
Центром окружности, вписанной в треугольник, является точка пересечения его биссектрис.
На рисунке приложения ОН=r; BO=6-r
По т.Пифагора найдем ВН=6
Проведем биссектрису АО.
Биссектриса угла треугольника делит противоположную этому углу сторону в отношении, равном отношению двух прилежащих сторон
ОН:ВО=АН:АВ
r:(6-r)=8:10 из пропорции следует
48-8r=10r откуда
18r=48
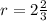
yA + yB +yC=180
yB=180-60-80=40
Рассмотрим треугольник BC1C
yC=yC1CA+yC1CB
yC1CA=yC1CB=40
yB=yC1CB=40
треугольник BC1C-равнобедренный.
CC1=BC1=6 см.
ответ:6 см.
Объяснение:
вроде бы правильно это сор же. по геометрии.