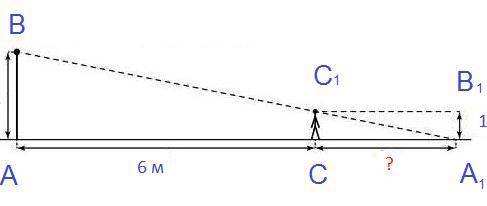
Объяснение: №1. Дано: АС=6 м, АВ=2,7 м, А₁В₁=0,9 м. Найти А₁С.
Решение (см рисунок к задаче):
△АA₁В подобен △CС₁A₁ (по двум углам: ∠ ВА₁А – общий, ∠ВАА₁=∠С₁СА₁=90 °)
В подобных треугольниках соответственные стороны пропорциональны, значит:
АA₁/A₁С=АВ/CC₁
Пусть А₁С=х, тогда АА₁=6+х, СС₁=А₁В₁=0,9
(6+х)/x=2,7/0,9
(6+х)/x=3
6+х=3х
2х=6
х=3 (м) длина тени
№2. Дано:ΔС₁О₁Р₁ подобен ΔСОР, СО=2,5, ОP
=2см, α =60°-угол между ними. k=3 Найти SΔС₁О₁Р₁
Решение: В условии видимо ОР=2 см, у вас с ошибкой записано условие, так как СО=ОС, такого быть не может, я так поняла)
Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия. т.е.:
S(ΔС₁О₁Р₁ )/ S( ΔСОР) = k² =3²=9.
Найдём площадь ΔСОР:
S(ΔСОР)=( 1/2) ·CO·OP·Sin60° =( 1/2) ·2,5·2·(√3/2) =2,5√3/2= 1,25·√3
тогда S(ΔС₁О₁Р₁ )= S(ΔСОР) ·k² = 1,25√3 ·9=11,25√3.
ответ: 11,25√3 см²
Объяснение:
Найдите углы ромба ABCD, если его диагонали AC И BD равны 4корень из 3 метров и 4 метра. (Для ясности нужно добавить фразу "О - точка пересечения диагоналей. ").
Решение: Пусть угол BAO=альфа. Диагонали ромба делят его углы ПОПОЛАМ, значит, угол DAO= углу BAO =альфа. Диагонали ромба взаимно ПЕРПЕНДИКУЛЯРНЫ, И ТОЧКОЙ ПЕРЕСЕЧЕНИЯ ДЕЛЯТСЯ ПОПОЛАМ, следовательно в прямоугольном треугольнике ABO катет AO равен 2*(корень из 3) метрАМ, а катет ВО равен 2 метрАМ. Поэтому тангенс альфа=1/(корень из 3), (Здесь нужно добавить, значит альфа равно 30 градусам) , а угол BAD=2*30= 60 градусам, угол ADC= (180 градусов минус угол ВАD)=120 градусам.
ответ 60 и 120 градусов (или Пи/3 и 2*Пи/3 радиан) .