Угол между меньшей диагональю и большей боковой
стороной раваен 90°.
Объяснение:
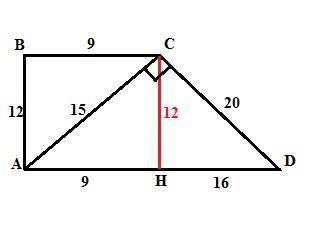
Пусть дана прямоугольная трапеция АВСD с прямыми углами А и В. В прямоугольном треугольнике АВС катет АВ по Пифагору равен
АВ = √(АС²-ВС²) = √(15²-9²) = 12 ед. Опустим высоту СН.
СН = АВ = 12 (противоположные стороны прямоугольника).
Тогда в прямоугольном треугольнике HCD по Пифагору:
НD = √(CD²-CH²) = √(20²-12²) = 16 ед.
AD = AH+HD = 9+16 = 25 ед.
В треугольнике АСD стороны равны:
АС=15ед, CD = 20ед, (дано), a AD = 25 ед (найдено выше).
Следовательно, треугольник АСD - прямоугольный с прямым углом ACD, так как выполняется условие AD² = AC²+CD² (проще говоря, треугольник Пифагоров с соотношением сторон 3:4:5).
ответ: угол между меньшей диагональю и большей боковой
стороной равен 90°.
Описанный четырёхугольник – это четырехугольник, имеющий вписанную окружность.
Обозначим стороны a,b,c,d.
В таком четырехугольнике суммы противополжных сторон РАВНЫ.
a+c =b+d (1)
по условию периметр P=a+c +b+d = 56
a+c = P/2 ; b+d = P/2
c = P/2 - a (2)
d = P/2 - b (3)
две его стороны равны 6 и 14
допустим это противоположные стороны 6+14=20 - НО это не половина периметра
значит стороны смежные , например a=6 ; b=14 (4)
тогда
подставим (4) в (2)(3)
c = P/2 - a = 56/2 - 6 =22
d = P/2 - b = 56/2 - 14 = 14
стороны 6;14;22;14
ответ большую из оставшихся сторон 22
6 см
Объяснение:
На фото