Question

Задано трикутник вершинами А(-2;3),В(0;1),С(4;-5).Знайти довжину і скласти рівняння медіани трикутника ,проведеної з вершини В.

Answer 1

ответ:  1. Знайдемо координати точки М, яка є серединою сторони АС за формулою ділення відрізка на дві рівні частини:

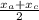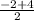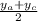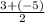Хм= $\frac{x_{a}+x_{c} }{2} \\$= $\frac{-2+4}{2}$=1;  Yм=$\frac{y_{a}+y_{c} }{2}$=$\frac{3+(-5)}{2}$= -1

Отже, координати точки М (1;-1).

2. Довжину медиани знайдемо, як відстань між двома точками за формулою:

BM =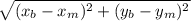 $\sqrt{(x_{b}-x_{m} )^{2} +(y_{b}-y_{m} )^{2} }$=$\sqrt{(0-1)^{2}+ (1-(-1))^{2} }$= $\sqrt{5}$ одиниць.

3. Рівняння медиани ВМ запишемо, скориставшисьформулою рівняння прямої, щопроходить через дві точки:

$\frac{x-x_{1} }{x_{2} -x_{1} }$  =  $\frac{y-y_{1} }{y_{2}-y_{1} }$

Підставивши координати точок В(0;1) і М(1;-1) запишемо загальне рівняння медиани ВМ:

$\frac{x-0}{1-0} =\frac{y-1}{-1-1}$  ;  

х=$\frac{y-1}{-2}$;

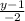-2х=у-1;

-2х-у+1=0.

Для знаходження рівняння з кутовим коефіцієнтом kВМ медиани ВМ, розв"яжемоотримане рівняння відносно у:

у= -2х+1, звідси k=-2.

Відповідь: довжина медиани$\sqrt{5}$ одиниць, загальне рівняння медиани -2х-у+1=0, рівняння з кутовим коефіцієнтом у=-2х+1.

Малюнок до задачі в додатку.

Объяснение: