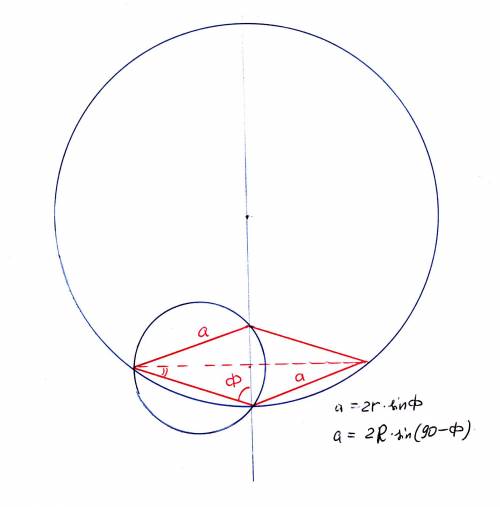
Меньшая окружность проходит через 3 вершины, одна из который - острый угол, а 2 - вершины тупых углов. Острый угол является вписанным в эту окружность. И, наоборот, большая окружность проходит через вершину острого угола, потом- тупого, и - опять острого. В большую окружность вписан тупой угол.
r = 5; R = 12; a = ?
Обозначим за Ф половину тупого угла ромба. В треугольнике, вписанном в малую окружность, это будет острый угол, противолежащий стороне а;
Тогда по теореме синусов
a = 2*r*sin(Ф); sin(Ф) = a/(2*r);
Для тупоугольного равнобедренного треугольника, вписанного в большую окружность, угол при основании (противолежащий стороне а) равен (180 - 2*Ф)/2 = 90 - Ф;
Поэтому по той же теореме синусов
a = 2*R*sin(90 - Ф) = 2*R*cos(Ф); cos(Ф) = a/(2*R);
Осталось возвести это в квадрат и сложить
1 = a^2/(2*r)^2 + a^2/(2*R)^2; (2/a)^2 = 1/r^2 + 1/R^2;
Нет смысла упрощать это выражение в общем виде, подставим числа.
2/a = корень(1/25 + 1/144) = 13/60; (опять пифагорова тройка 5,12,13)
a = 120/13;
В обратной теореме вывод и посылка меняются местами.
Это получается правильно в тех случаях, когда имеется однозначное соответствие между посылкой и выводом, то есть первое без второго не бывает, как и второе без первого.
Но есть случай формулировки когда отсутствию первого всегда соответствует отсутствие второго. Это тоже один из вариантов формулировки обратной теоремы - противоположная теорема.
И при этом также есть взаимно однозначное соответствие.
В обеих теоремах должен реализоваться принцип необходимости и достаточности.
Свойства о которых говорится в посылке необходимы и достаточны для наличия свойств оо которых говорится в выводе, и наоборот.
Это и есть вхзаимное соответстствие.
Обратная теорема
Обратная теорема, теорема, условием которой служит заключение исходной (прямой) теоремы, а заключением — условие. Обратной к О. т. будет исходная (прямая) теорема. Таким образом, прямая и О. т. взаимно обратны. Например, теоремы: "если два угла треугольника равны, то их биссектрисы равны" и "если две биссектрисы треугольника равны, то соответствующие им углы равны" — являются обратными друг другу. Из справедливости какой-нибудь теоремы, вообще говоря, не следует справедливость обратной к ней теоремы. Например, теорема: "если число делится на 6, то оно делится на 3" — верна, а О. т. : "если число делится на 3, то оно делится на 6" — неверна. Даже если О. т. верна, для её доказательства могут оказаться недостаточными средства, используемые при доказательстве прямой теоремы. Например, в евклидовой геометрии верны как теорема "две прямые на плоскости, имеющие общий перпендикуляр, не пересекаются", так и обратная к ней теорема "две непересекающиеся прямые на плоскости имеют общий перпендикуляр". Однако вторая (обратная) теорема основывается на евклидовой аксиоме параллельных, тогда как для доказательства первой эта аксиома не нужна. В Лобачевского геометрии вторая просто неверна, тогда как первая остаётся в силе. О. т. равносильна теореме, противоположной к прямой, т. е. теореме, в которой условие и заключение прямой теоремы заменены их отрицаниями. Поэтому прямая теорема равносильна теореме, противоположной к обратной, т. е. теореме, утверждающей, что если неверно заключение прямой теоремы, то неверно и её условие. Известный "доказательства от противного" как раз и представляет собой замену доказательства прямой теоремы доказательством теоремы, противоположной к обратной. Справедливость обеих взаимно обратных теорем означает, что выполнение условия любой из них не только достаточно, но и необходимо для справедливости заключения