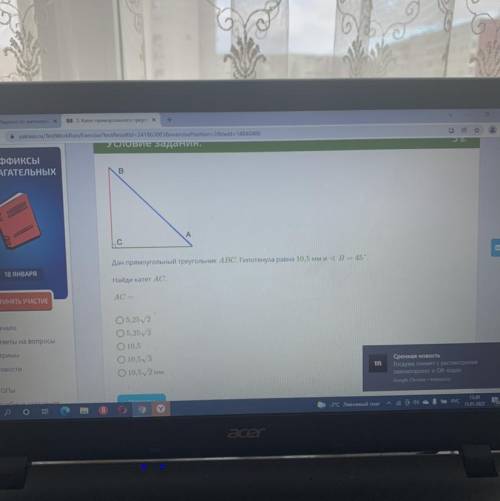
Объяснение:
Катеты АВ и АС равны (ΔА=∠В), по т. Пифагора:
2а²=с², 2а²=10,5², а=√(10,5²/2)=10,5/√2=5,25√2=АС.
ответ:Cм рисунок в приложении. Проведем высоты вы трапеции из вершин верхнего основания. Обозначим нижнее основание и боковые стороны х
Из прямоугольных треугольников находим катет
Катет равен гипотенузе х, умноженной на косинус 65°
(если бы 60°, то косинус 60° равен 0,5)
Тогда нижнее основание состоит их трех отрезков:
х·cos 65°+x+x·cos 65°=16 ⇒ x=16:(2cos 65°+`1)
cos 65°≈ 0,423
0,423х+х+0,423х=16
1,846 х=16
х≈8,67
Р≈8,67+8.67+8.67+16=42,01
Если все-таки 60° угол, то все гораздо проще:
0,5х+х+0,5х=16
2х=16
х=8
Р=8+8+8+16=40
Cм рисунок в приложении. Проведем высоты вы трапеции из вершин верхнего основания. Обозначим нижнее основание и боковые стороны х
Из прямоугольных треугольников находим катет
Катет равен гипотенузе х, умноженной на косинус 65°
(если бы 60°, то косинус 60° равен 0,5)
Тогда нижнее основание состоит их трех отрезков:
х·cos 65°+x+x·cos 65°=16 ⇒ x=16:(2cos 65°+`1)
cos 65°≈ 0,423
0,423х+х+0,423х=16
1,846 х=16
х≈8,67
Р≈8,67+8.67+8.67+16=42,01
Если все-таки 60° угол, то все гораздо проще:
0,5х+х+0,5х=16
2х=16
х=8
Р=8+8+8+16=40
Мы можем рассмотреть наш треугольник как половину квадрата, разрезанную по диагонали (именно квадрата, потому что прямоугольный треугольник с острым углом в 45° – ещё и равнобедренный), => ВС=АС=АВ/√2=(10,5)/√2=(10,5√2)/2=5,25√2
Можно было бы, конечно, и через теорему Пифагора, но там было бы чуть большее решение