Внутри треугольника авс взята такую точку м, что угол смв = 100 градусов. срединные перпендекуляры к вм и см пересекают соответствующие стороны ав и ас в точках p и q. точки p, q и м лежат на одной прямой. найдите величину угла сав.

👇

Ответ:

azim20071

03.03.2020

1) сумма углов MBC и MCB = 180° - 100° = 80°;
2) треугольники BPM и CQM равнобедренные (BP = PM и CQ = QM),
поэтому сумма углов PBM и QCM равна сумме углов PMB и QMC, то есть опять 80°, поскольку угол PMQ = 180°;
получилось, что в треугольнике ABC сумма углов при стороне BC равна 80° + 80° = 160°;
третий угол равен 180° - 160° = 20°

4,6(45 оценок)

Открыть все ответы

Ответ:

maslyuk05

03.03.2020

Первый признак параллельностиПрямые параллельны, если при пересечении их третьей прямой, образуемые внутренние углы, лежащие накрест, будут равны.Допустим, при пересечении прямых АВ и СD прямой линией ЕF, были образованы углы /1 и /2. Они равны, так как прямая линия ЕF проходит под одним уклоном по отношению к двум остальным прямым. В местах пересечения линий, ставим точки Ки L – у нас получился отрезок секущей ЕF. Находим его середину и ставим точку О (черт. 189).На прямую АВ опускаем перпендикуляр из точки О. Назовем его ОМ. Продолжаем перпендикуляр до тех пор, пока он не пересечется с прямой СD. В результате, первоначальная прямая АВ строго перпендикулярна МN, а это значит, что и СD_|_МN, но это утверждение требует доказательства. В результате проведения перпендикуляра и линии пересечения, у нас образовалось два треугольника. Один из них – МОЕ, второй – NОК. Рассмотрим их более подробно. признаки параллельности прямых 7 классДанные треугольники равны, поскольку, в соответствии с условиями теоремы, /1 =/2, а в соответствии с построением треугольников, сторона ОK = стороне ОL. Угол МОL =/NОК, поскольку это вертикальные углы. Из этого следует, что сторона и два угла, прилежащие к ней одного из треугольников соответственно равны стороне и двум углам, прилежащим к ней, другого из треугольников. Таким образом, треугольник МОL =треугольникуNОК, а значит, и угол LМО = углу КNО, но нам известно, что/LМО прямой, значит, и соответствующий ему, угол КNО тоже прямой. То есть, нам удалось доказать, что к прямой МN, как прямая АВ, так и прямая СD перпендикулярны. То есть, АВ и СD по отношению друг к другу являются параллельными. Это нам и требовалось доказать. Рассмотрим остальные признаки параллельности прямых (7 класс), которые отличаются от первого признака по доказательства.Второй признак параллельностиСогласно второму признаку параллельности прямых, нам необходимо доказать, что углы, полученные в процессе пересечения параллельных прямых АВ и СD прямой ЕF, будут равны. Таким образом, признаки параллельности двух прямых, как первый, так и второй, основывается на равности углов, получаемых при пересечении их третьей линией. Допускаем, что /3 = /2, а угол 1 = /3, поскольку он вертикален ему. Таким образом, и /2 будет равен углу1, однако следует учитывать, что как угол 1, так и угол 2 являются внутренними, накрест лежащими углами. Следовательно, нам остается применить свои знания, а именно то, что два отрезка будут параллельными, если при их пересечении третьей прямой образованные, накрест лежащие углы будут равными. Таким образом, мы выяснили, что АВ || СD.Нам удалось доказать, что при условии параллельности двух перпендикуляров к одной прямой, согласно соответствующей теореме, признак параллельности прямых очевиден.Третий признак параллельностиСуществует еще и третий признак параллельности, который доказывается посредством суммы односторонних внутренних углов. Такое доказательство признака параллельности прямых позволяет сделать вывод, что две прямые будут параллельны, если при пересечении их третье прямой, сумма полученных односторонних внутренних углов, будет равна 2d. См. рисунок 192.
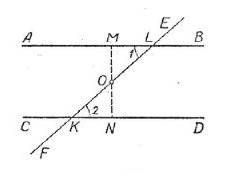
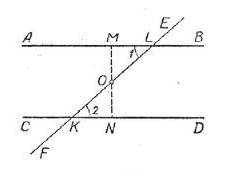
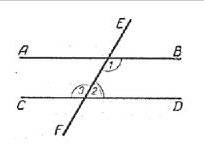
Напишите теорему по 7 класс тема: признак параллельности напишите

Напишите теорему по 7 класс тема: признак параллельности напишите

4,6(10 оценок)

Ответ:

орпасм

03.03.2020

При центральной симметрии отрезок отображается в равный и параллельный ему отрезок.

Стороны шестиугольника А₁А₂ и А₄А₅ равны и параллельны, значит эти отрезки центрально-симметричны. Центр симметрии - точка пересечения отрезков А₁А₄ и А₂А₅ - точка О. По определению центральной симметрии точка О - середина этих отрезков.

Аналогично, отрезки А₂А₃ и А₅А₆ центрально-симметричны относительно точки пересечения отрезков А₂А₅ и А₃А₆, которая является их серединой. Но середина отрезка А₂А₅ - точка О, значит точка О и середина отрезка А₃А₆. Итак, все диагонали пересекаются в одной точке.

4,6(28 оценок)

Это интересно:

Финансы-и-бизнес

18.09.2022

Как вычислить период оборота запасов: практическое руководство...

19.11.2022

Как избавиться от одержимости человеком: советы от психологов и опытных людей...

Образование-и-коммуникации

04.01.2021

Как узнать, который час по-испански: простые правила для изучения...

Мир-работы

14.09.2021