1)
полная окружность 360 град ; 9/11 - всего 20 частей
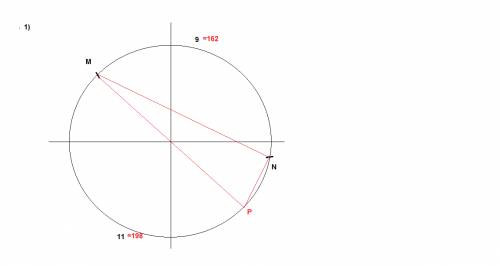
дуга (9) = 9/20*360=162 град
дуга (11) =11/20*360=198 град
вершина N- лежит на окружности
сторона MP- совпадает с диагональю
свойство прямоугольного треугольника , вписанного в окружность
треугольник МNP - прямоугольный
<MNP=90 град
<MPN (вписанный)-опирается на дугу MN=162 град
свойство вписанного угла (он равен половине дуги, на которую опирается)
<MPN=1/2*162=81 град
<NMP=90- <NPM=90-81=9 град
ответ углы 90 ;81;9 град
На мой взгляд самый быстрый построить угол 30 градусов с линейки и циркуля состоит в следующем:
проводим горизонтальную линию, ставим на нее в произвольной точке циркуль и проводим окружность. В точке, где окружность пересекла линию (например справа) опять ставим циркуль и проводим еще одну такую же окружность. Проводим линию через центр первой окружности и точку пересечения окружностей (красная линия) и проводим линию через точки пересечения окружностей (зеленая линия). Острый угол между красной и зеленой линиями равен 30 градусам.
Уточнение к условию. Пирамида не может быть одновременно и правильной, и прямоугольной. У правильной пирамиды в основании лежит правильный многоугольник, а боковые грани - равные равнобедренные треугольники. У прямоугольной пирамиды одно из боковых ребер перпендикулярно основанию. Поэтому две боковые грани будут прямоугольными треугольниками, а остальные - разносторонними треугольниками в общем случае. В условии задачи речь идёт о правильной пирамиде, в основании которой лежит квадрат.
Сторона основания правильной четырёхугольной пирамиды равна 6 см, а высота пирамиды √13 см. Найти длину бокового ребра.
Дана пирамида MABCD, AB=BC=CD=AD = 6 см; MO = √13 см.
Найти: AM=BM=CM=DM - ?
Высота правильной четырехугольной пирамиды опускается в точку пересечения диагоналей основания-квадрата. Диагональ квадрата
AC = AB · √2 = 6√2 см
Диагонали квадрата делятся точкой пересечения пополам.
AO = OC = AC : 2 = 6√2 : 2 = 3√2 см
ΔMOC - прямоугольный. Теорема Пифагора
MC² = MO² + OC² = (√13)² + (3√2)² = 13 + 18 = 31
MC = √31 см
ответ: боковое ребро пирамиды равно √31 см