

Дано:
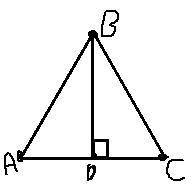
ABC - треугольник.
BD - медиана
BD ⊥ AC
Доказать: ABC - равнобедренный
1) Т.к BD-медина, перпендикулярная AC, то она является высотой.
2) Т.к BD- медиана и высота, то по утверждению "В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой" треугольник ABC равнобедренный, что и требовалось доказать.
Вот алгоритм
Объяснение:
Алгоритм определения вида придаточного предложения
1. Определите главную часть сложноподчинённого предложения.
2. Определите опорное слово в главной части (если оно есть).
3. Задайте вопрос от главной части к придаточному предложению:
а) от содержания главной части в целом;
б) от сказуемого в главной части;
в) от существительного или местоимения в
главной части;
г) невозможно задать вопрос к придаточному (при присоединительных и сопоставительных).
4. Укажите средства связи в придаточной части (союзы или союзные слова).
5. Назовите вид придаточного предложения
выделим полные квадраты [4x^2+16x+16]+[y^2-2y+1]-16-1+15=0
4(x+2)^2+(y-1)^2=2 -эллипс ,координаты центра х=-2;у=1
2х + у + 5 = 0 --->y= -2x-5>k1= -2
Для перпендикуляра k2=-1/k1=-1/-2=0.5
уравнение у=k2*x+b>1=0.5*(-2)+b>b=2
ответ :у=0.5х+2 или х-2у+4=0