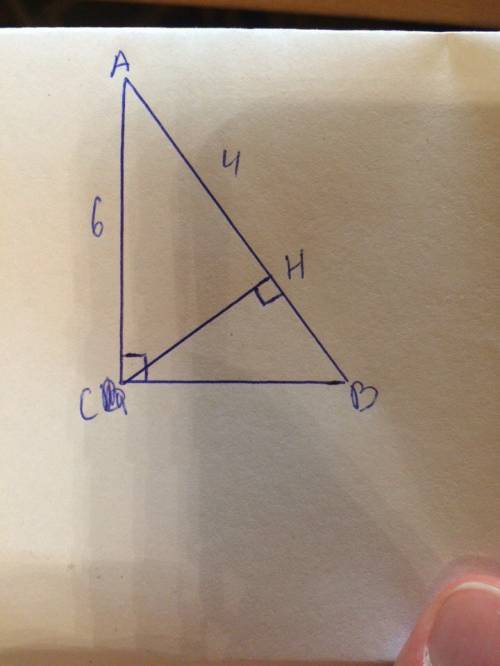
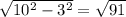. Значит, вся диагональ -- 
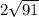, а сторона квадрата, которая в 
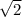раз меньше, чем диагональ, равна 
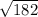. Таким образом, боковая грань представляет собой треугольник со сторонами 10, 10, 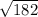. Площадь этого треугольника можно найти, например, опустив высоту из вершины, (эта высота будет и медианой). Получается, высота равна 
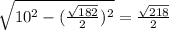, откуда площадь одного треугольника равна 
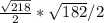, а площадь боковой поверхности равна площади четырёх таких треугольников, т. е. 
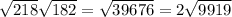Может, обсчитался где-то.
d=10
H=V13^2-(d/2)^2
H=V169-25
H=12
ответ:12