∠АВС = 20°.
Объяснение:
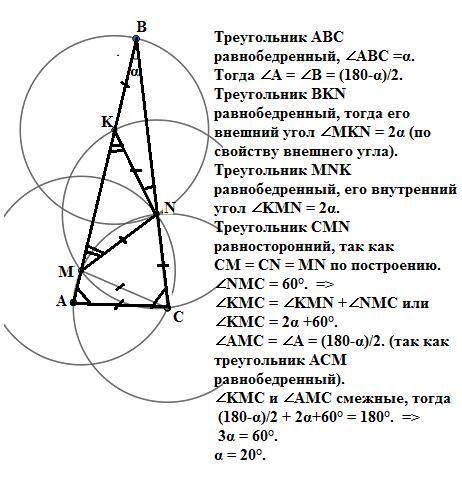
Треугольник АВС равнобедренный, ∠ABC =α.
Тогда ∠A = ∠В = (180-α)/2.
Треугольник BKN равнобедренный, тогда его внешний угол
∠MKN = 2α (по свойству внешнего угла).
Треугольник MNK равнобедренный, его внутренний угол
∠KMN = 2α.
Треугольник CMN равносторонний, так как
CM = CN = MN по построению.
∠NMС = 60°. =>
∠KMC = ∠KMN +∠NMС или
∠KMC = 2α +60°.
∠АMС = ∠A = (180-α)/2. (так как треугольник АСМ равнобедренный).
∠KMС и ∠АMС смежные, тогда
(180-α)/2 + 2α+60° = 180°. =>
3α = 60°.
α = 20°.
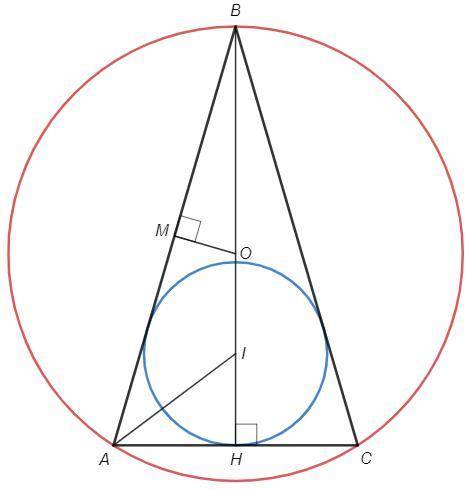
Равнобедренный треугольник, основание AC=14.
BH - высота к основанию, является также биссектрисой и медианой.
AH=AC/2 =7 (H - середина AC)
BH =√(AC^2 -AH^2) =24 (теорема Пифагора)
S(ABC) =AC*BH/2 =14*24/2 =168
Центр вписанной окружности (I) - точка пересечения биссектрис.
BI/IH =AB/AH =25/7 (теорема о биссектрисе)
IH =7/32 BH =21/4 =5,25
(IH - расстояние от центра до стороны, то есть радиус)
Центр описанной окружности (O) - точка пересечения серединных перпендикуляров.
M - середина AB, BM=25/2
△OBM~△ABH (по двум углам)
OB/AB =BM/BH
OB =25*25/2*24 =625/48 ~13,02
sin45° = 2/√2
tg60° = √3
tg180° = tg0° = 0
2. sin120° = sin(180° - 120°) = sin60° = √3/2
cos150° = -cos(180° - 150°) = -cos30° = -√3/2
sin135° = sin(180° - 135°) = sin45° = √2/2
3. Теорема синусов:
AB/sinC = BC/sinA = AC/sinB
Теорема косинусов:
AC² = AB² + BC² - 2AB•BC•cosB
AB² = AC² + BC² - 2AC•BC•cosC
BC² = AC² + AB² - 2AB•AC•cosA
4. Углом между их направлениями.
5. Произведение их абсолютных величин на косинус угла между ними.
6. Если их скалярное произведение равно 0 (или угол между их направлениями равен 0).
7. Когда их скалярное произведение равно 0.
8. Координаты вектора k{x1; y1}, координаты вектора n{x2; y2}.
cosB = (x1•x2 + y1•y2)/((√x1² + y1²)•(√x2² + y2²))