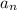- угол, n - количество сторон.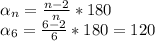 
. 
.
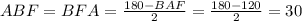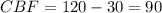Итак у нас две медианы, каждая из них делится точкой пересечения в отношении 2:1 считая от вершины.
Т.е. Каждую медиану разделили на три части, две части от вершины до точки пересечения и одна от точки пересечения до стороны
МР=12; делим на три, получаем 12:3=4-одна часть, 4*2=8-две части, т.о. МО=8, ОР=4
NE=15; делим на три, получаем 15:3=5 -одна часть, 5*2=10 -две части, т.о. NО=10, ОЕ=5
Теперь треугольник МОЕ, он прямоугольный, с катетами 8 и 5 , площадь прямоугольного треугольника равна половине произведения катетов, т.е. 8*5:2=20
Медиана прямоугольного треугольника, проведенная из вершины прямого угла, равна половине гипотенузы.
ВM = AC/2 , BM = AM = MC ⇒ ΔABM - равнобедренный
∠МАВ = ∠АВМ = 46°
В ΔАВН (∠АНВ = 90°)
∠АВН = 90° - ∠ВАН = 90° - 46° = 44°
Тогда, ∠МВН = ∠АВМ - ∠АВН = 46° - 44° = 2°
ответ: 2°.