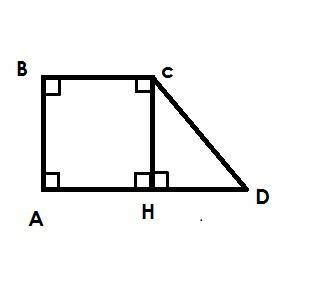
1. По катету и гипотенузе (PAD=DCB)
2. По двум катетам (MKT=NKT)
3. По катету и гипотенузе, по 2 катетам, острому углу (PSK=RSK)
4. По гипотенузе и острому углу (ERF=ESF)
5. По катету и гипотенузе (Если SPM=TKM) По двум катетам (Если SRM=TRM)
6. По катету и гипотенузе (Если AED=BFD) По двум катетам (Если ACD=BCD)
7. прости, не знаю
8. ...
9. По катету и стороне (не уверена) (ADE=BFM)
10. По двум катетам (ADB=CBD)
Объяснение:
в 3 задании т.к. углы при основании PR равны, то прямоугольник равнобедренный, а значит треугольники прямоугольные, а KS делит основание напополам и их равенство можно доказать по 2 катетам, так как стороны боковые равны будут можно по катету и гипотенузе или же по гипотенузе и острому углу.
в 5 и 6 задании т.к. маленькие треугольники равны, то и углы при основании равны, а значит 2 треугольника в которых маленькие тоже прямоугольные.
Элементы произвольного треугольника ABC обычно обозначаются так:
BC, CA, AB — стороны;
a, b, c — их длины;
α, β, γ — величины противолежащих углов;
ha, ma, la — высота, медиана и биссектриса, выходящие из вершины A;
R — радиус описанной окружности,
r — радиус вписанной окружности;
S — площадь,
p — полупериметр.
Отметим, что в отдельных задачах обозначения могут отличаться от стандартных.
Теорема 1 (теорема Пифагора). В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы, то есть
c2 = a2 + b2,
где c — гипотенуза треугольника.
Теорема 2. Для прямоугольного треугольника (рис. 1) верны следующие соотношения:
a = c cos β = c sin α = b tg α = b ctg β,
где c — гипотенуза треугольника.
Теорема 3. Пусть ca и cb — проекции катетов a и b прямоугольного треугольника на гипотенузу c, а h — высота этого треугольника, опущенная на гипотенузу (рис. 2). Тогда справедливы следующие равенства:
h2 = ca∙cb, a2 = c∙ca, b2 = c∙cb.
Теорема 4 (теорема косинусов). Для произвольного треугольника справедлива формула
a2 = b2 + c2 – 2bc cos α.
Теорема 5. Около всякого треугольника можно описать окружность и притом только одну. Центр этой окружности есть точка пересечения серединных перпендикуляров, проведенных к сторонам. Центр описанной окружности лежит внутри треугольника, если треугольник остроугольный; вне треугольника, если он тупоугольный; на середине гипотенузы, если он прямоугольный (рис. 3).
Теорема 6 (теорема синусов). Для произвольного треугольника (рис. 4) справедливы соотношения
Теорема 7. Во всякий треугольник можно вписать окружность и притом только одну (рис. 5).
Центр этой окружности есть точка пересечения биссектрис трех углов треугольника. Центр вписанной окружности лежит всегда внутри треугольника.
Теорема 8 (формулы для вычисления площади треугольника).
4
Последняя формула называется формулой Герона.
Теорема 9 (теорема о биссектрисе внутреннего угла).
Биссектриса внутреннего угла треугольника (рис. 6) делит противоположную сторону на части, пропорциональные прилежащим сторонам треугольника, то есть
b : c = x : y.
Теорема 10 (формула для вычисления длины биссектрисы) (см. рис. 6)
.
Теорема 11 (формула для вычисления длины биссектрисы).
Теорема 12. Медианы треугольника пересекаются в одной точке и делятся в этой точке на отрезки, длины которых относятся как 2 : 1, считая от вершины (рис. 7).
Теорема 13 (формула для вычисления длины медианы).
Доказательства некоторых теорем
Доказательство теоремы 10. Построим треугольник ABC и проведем в нем биссектрису AD (рис. 8). Пусть CD = x и DB = y. Применим к треугольникам ABD и ACD теорему косинусов:
BD2 = AB2 + AD2 – 2∙AB∙AD∙cos ∠BAD;
CD2 = AC2 + AD2 – 2∙AC∙AD∙cos ∠CAD.
Или, что то же самое,
Выразим из каждого неравенства и приравняем полученные результаты:
Применив теперь к треугольнику ABC теорему о биссектрисе внутреннего угла, получим, что