2) ММ1 = (АА1+ВВ1) \2=10 м
3) прямая, проходящая через чентры сторон - средняя линия и параллельна основанию (АВ)
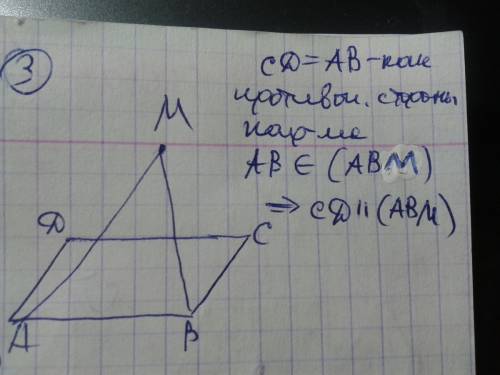
т.к. АВ параллельно СД то и прямая параллельна основанию
В треугольнике АЕВ линия соединяющая серидины двух сторон является средней линией треугольника, а по свойствам, средняя линия треугольника параллельна основанию(т.е. АВ). А АВ параллельна СD. Из чего следует, что средняя линия треугольника параллельна CD.
Доказательнство,
1)прямая KF- средняя линия в треугольнике АЕВ ( так как К-середина отрезка ЕА, а F-середина ЕВ)
2)следовательно KF||FB-по свойству средней линиии(средняя линия в треугольнике параллельна основанию треугольника)
3) ТАк как AB|| CD( по свойству параллелограмма), а KF||AB то KF||CD
что и требовалось доказать!

Пусть МК - отрезок, соединяющий середины АЕ и ВЕ.
Тогда МК - средняя линия тр-ка АВЕ.
Значит МК //АВ, но АВ // СД
Следовательно, МК//СД, что и треб. доказать.


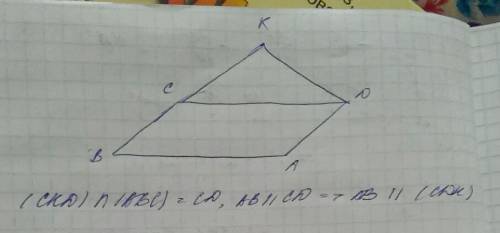
2)АВ параллельна СД, значит по признаку параллельности прямых ТR параллельна СД.
ДОКАЗАНО