Саму задачу можно переформулировать немного по-другому:
Было: Расставить минимальное количество шашек на шахматной доске 8 на 8, так чтобы было невозможно поставить коня так, чтобы он не бил ни одной шашки.Переходит в: расставить на доске минимальное количество коней так, чтобы было невозможно поставить шашку не под удар коня.Если мы решим вторую задачу, то просто нужно будет заменить коней шашками - и мы получим искомое расположение.
По поводу второй задачи можно заметить, что:
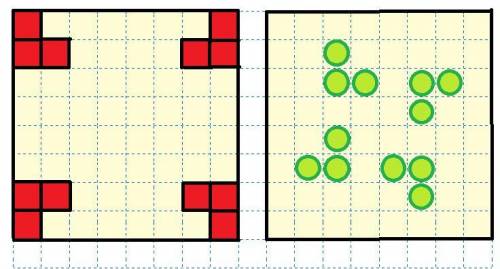
Разные кони должны бить выделенные красным клетки на рисунке ниже.Отсюда следует, что мы не можем расставить менее, чем 4 * 3 = 12 коней. Если это можно сделать, то задача решится. И да, это получилось сделать (рисунок 2).
Заменяем коней шашками и получаем ответ: 12 коней.
ответ: 12 шашек.
ответ: а) 1 целая 3/8 б) -1/2
Пошаговое объяснение:
а) 1. Найдём разность дробей с равными знаменателями:
5/8 - 16/8 = 5-16 / 8 = - 11/8
2. Так как числитель больше знаменателя, то преобразуем неправильную дробь в смешанное число:
11/8 = 1*8+3 / 8 = 1*8 / 8 + 3/8 = 1 + 3/8
б) 1. Раскроем скобки возле второй дроби:
2 21/26 + (-3 4/13) = 2 21/26 - 3 4/13
2. Преобразуем смешанные числа в неправильные дроби:
первое:
2 21/26 = 21+2*26 / 26 = 73/26
второе:
3 4/13 = 4+3*13 / 13 = 43/13
3. Приведем дроби к наименьшему общему знаменателю:
Найдем наименьшее общее кратное знаменателей дробей 73/26 и 43/13
НОК(26,13) = 26
26/26 = 1 — дополнительный множитель первой дроби
26/13 = 2 — дополнительный множитель второй дроби
73/26 = 73*1 / 26*1 = 73/26
43/13 = 43*2 / 13 * 2 = 43/26
4. Найдем разность дробей с равными знаменателями:
73/26 - 86/26 = 73-86 / 26 = -13/26
5. Упростим дробь:
-13/26 = - 1*3 /2*13 = - 1/2