Пусть: x - яблоки, шт.;
y - груши, шт.;
z - апельсины, шт.
Тогда, по условию:
0,5x + 3y + 5z = 100
x + y + z = 100
Умножим первое уравнение на 2 и вычтем из него второе уравнение почленно. Получим:
5y + 9z = 100
y = 20 - 9z/5
Т. к. количество фруктов должно быть числом целым и не отрицательным, то для последнего уравнения z должно быть кратным 5 и таким, чтобы 9z/5 было бы меньше 20. Этому условию удовлетворяет z = 5 и z = 10:
z = 5 => y = 20 - 9z/5 = 20 - 9•5/5 = 11
x = 100 - y - z = 100 - 11 - 5 = 84
z = 10 => y = 20 - 9z/5 = 20 - 9•10/5 = 2
x = 100 - y - z = 100 - 2 - 10 = 88
ответ: 1) яблок: 84 шт,
груш: 11 шт,
апельсинов: 5 шт.
или: 2) яблок: 88 шт,
груш: 2 шт,
апельсинов: 10 шт.
ответ: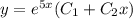
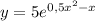
Пошаговое объяснение:
Определить общее решение дифференциального уравнения:
y" - 10y' + 25y = 0.
Решение
Характеристическое уравнение имеет вид:
k² - 10k + 25 = 0
(k - 5)² = 0
k₁ = k₂ = 5
Корни действительные и равные k₁ = k₂ = k . В этом случае общее решение уравнения:
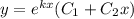
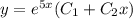
Определить частное решение дифференциального уравнения:
y'+y=xy, удовлетворяющее начальному условию y(2)=5.
Решение
y' + y = xy
y' = xy - у
Делим обе части уравнения на у
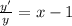
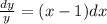
Интегрируем обе части уравнения
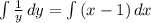
ln|y| -lnC = 0.5x² - x
Запишем общее решение ДУ
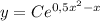
Найдем частное решение ДУ подставив начальные условия y(2)=5
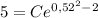
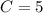
Поэтому частное решение ДУ
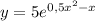
Пошаговое объяснение:
35y=1,2+12,8
35y=14
y=14:35
y=0,4
5y<2
y=2:5
y=0,4