не может.
Пошагово
Для ответа на вопрос задачи нам нужно вспомнить несколько определений:
1. Простым числом называется число, которое можно разделить без остатка только на единицу или на само себя.
2. Натуральным числом называется число, полученное в результате естественного счета чего либо целого. То есть любое натуральное число будет целым по определению.
3. Объем прямоугольного параллелепипеда, а значит и его частного случая - куба, определяется как произведение длин всех трех измерений. Для куба он выражается как значение длины ребра в третьей степени.
Невозможно извлечь кубический корень из простого числа, чтобы в результате получить натуральное число.
Пошаговое объяснение:
Введем замену 
; 
.
Уравнение примет вид
Далее заметим, что для любого 
верно 
. То есть верхнее ограничение 
выполняется автоматически. Значит, полученная задача равносильна задаче о решении уравнения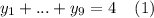 
в целых неотрицательных числах.
А для такой задачи применим метод шаров и перегородок: количество решений уравнения (1) совпадает с количеством размещений 4 неразличимых шаров в 9 ящиках [или, что то же самое, с количеством разделения ряда из 4 шаров 8 перегородками].
Искомое количество вариантов
Т.к. трапеция прямоугольная, то меньшая боковая сторона является и высотой.
Площадь трапеции находят по формуле S = (a + b)h/2. где a и b - основания, h - высота или S = mh, где m - средняя линия, h - высота.
Т.к. по условию S = 42 см², m = 7 см, то h = 42 : 7 = 6 (см).
Значит, меньшая боковая сторона трапеции равна 6 см.
ответ: 6 см.