60
Объяснение:
Если обозначить прямоугольник АВСД
а серединный перпендикуляр к диагонали AC - ОК.
Точка К-принадлежит стороне ВС
Точка О-точка пересечения диагоналей АС и ВД (она же середина этих диагоналей)
Для решения просто проведем прямую параллельно основанию АД через
точку пересечения диагоналей АС и ВД.
Она пересекает стороны АВ и СД в точках Н и М.
Обозначим угол пересечения диагоналей СОД = а
В треугольнике СОМ угол СОМ равен половине угла пересечения диагоналей a/2
В прямоугольном треугольнике КОС угол ОСК также равен a/2
По условию угол ОКС = a
Сумма углов в треугольнике равна 180 градусам.
Следовательно можно записать
90+a+a/2=180
(3/2)a=90
a=60 градусов.
ответ: 60 градусов
60
Объяснение:
Если обозначить прямоугольник АВСД
а серединный перпендикуляр к диагонали AC - ОК.
Точка К-принадлежит стороне ВС
Точка О-точка пересечения диагоналей АС и ВД (она же середина этих диагоналей)
Для решения просто проведем прямую параллельно основанию АД через
точку пересечения диагоналей АС и ВД.
Она пересекает стороны АВ и СД в точках Н и М.
Обозначим угол пересечения диагоналей СОД = а
В треугольнике СОМ угол СОМ равен половине угла пересечения диагоналей a/2
В прямоугольном треугольнике КОС угол ОСК также равен a/2
По условию угол ОКС = a
Сумма углов в треугольнике равна 180 градусам.
Следовательно можно записать
90+a+a/2=180
(3/2)a=90
a=60 градусов.
ответ: 60 градусов
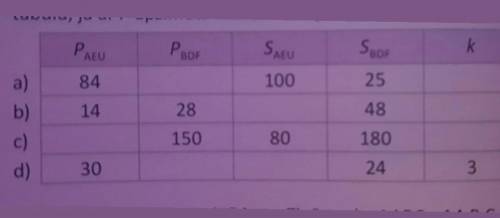
a) 84-42-100-25-2
b) 14-28-12-48-0.5
c) 100-150-80-180-2/3
d) 30-10-216-24-3
Объяснение:
AE=k*BD, EU=k*DF, AU=k*BF
Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.
100/25=4=2², т.е. коэффициент подобия равен двум, значит, стороны первого треугольника в два раза больше сторон второго треугольника, тогда периметр первого треугольника в два раза больше периметра второго треугольника: 84/2=42
Сторона первого треугольника в два раза меньше стороны второго треугольника, значит, площадь первого треугольника в 4 раза меньше площади второго треугольника.
14/28=0,5; 0,5²=0,25; 0,25*48=12
Площадь первого треугольника относится к площади второго треугольника как 80/180=4/9. Значит, коэффициент подобия равен корню из этого значения √4/9=2/3. Т.е. периметр первого треугольника составляет 2/3 периметра второго треугольника: 2/3*150=100
Коэффициент подобия равен 3, значит, стороны первого треугольника в три раза больше сторон второго треугольника. Значит, периметр первого в три раза больше периметра второго, а площадь первого в 3²=9 раз больше площади второго треугольника.
30/3=10; 24*9=216