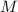Втреугольнике мкf сторона кf в 2 раза больше медианы мд чему равен угол м

👇

Ответ:

ololsha99

04.03.2021

Раз МД - медиана, то КД = ДФ = КФ/2,
а раз КФ = 2МД, то КД = ДФ = МД

дальше построим на КФ, как на диаметре окружность, ее центром будет пункт Д
раз КД = ДФ = МД = КФ/2 то КД, ДФ и МД - радиусы ⇒ точка М лежит на окружности ⇒ <M = 90 гр., так как он опирается на диаметр КФ

4,7(92 оценок)

Открыть все ответы

Ответ:

1234567891251

04.03.2021

1)Попробуем так , продолжим точку за

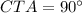, как выглядит на рисунку , так как CTA=90а

, то около треугольника можно описать окружность такая что

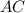будет диаметром ,

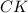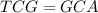биссектриса ,то TCG=GCA

, прямоугольник AGCE

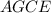в нем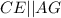

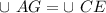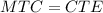, следовательно $\cup \ AG=\cup \ CE$ ; MTC=CTE

;

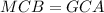откуда следует что равны по соответствующим дугам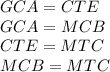
$GCA=CTE\\
GCA=MCB\\
CTE=MTC\\
MCB=MTC$
вся это конструкция выглядит довольно очень искусственно, имеется ввиду что исходя из того что AGCE

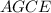является прямоугольник, авторы задачи видимо на этом и конструировали эту самую задачу.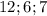

2)Теперь докажем численно , то есть для произвольного треугольник, что это и будет выполнятся , к примеру треугольник со сторонами 12;6;7

такой треугольник существует исходя из неравенств треугольников (Можно конечно взять стороны за a;b;c

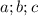и проделать операций которые описаны ниже,но оно будет объемным)
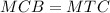Докажем так предположим что MCB=MTC

, то есть что это действительно так , тогда должно выполнятся условие 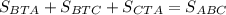$S_{BTA}+S_{BTC}+S_{CTA}=S_{ABC}$ , если это не так то предположение будет не верным , значит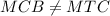 $MCB \neq MTC$
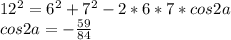
$12^2=6^2+7^2-2*6*7*cos2a\\
 cos2a=-\frac{59}{84}$
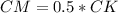по формуле биссектрисы , и зная что CM=0.5*CK

, можно найти по формуле биссектрисы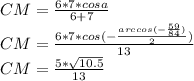
$CM=\frac{6*7*cosa}{6+7}\\
 CM=\frac{6*7*cos(-\frac{arccos(-\frac{59}{84})}{2})}{13}\\ 
 CM=\frac{5*\sqrt{10.5}}{13}$
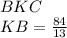
По теореме косинусов из треугольника $BKC\\
KB=\frac{84}{13}$
Найдем длину медианы $BM=\frac{\sqrt{2*KB^2+2*BC^2-CK^2}}{2}\\
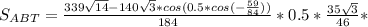
BM=\frac{24\sqrt{14}}{13}$ $S_{ABT}=\frac{339\sqrt{14}-140\sqrt{3}*cos(0.5*cos( -\frac{59}{84}))}{184} *0.5*\frac{35\sqrt{3}}{46}*$
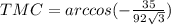Угол $TMC=arccos( - \frac{35}{92\sqrt{3}})$ (это когда находя угол BMC

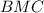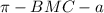, затем отнимая от $\pi-BMC-a$ )
Из треугольника TMC

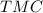, по теореме синусов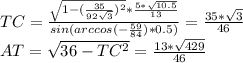
$TC=\frac{\sqrt{1-(\frac{35}{92\sqrt{3}})^2}*\frac{5*\sqrt{10.5}}{13}}{sin(arccos(-\frac{59}{84})*0.5)}=\frac{35*\sqrt{3}}{46}\\
AT=\sqrt{36-TC^2} = \frac{13*\sqrt{429}}{46}$
найдем

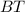по теореме косинусов так же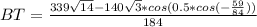
$BT=\frac{339\sqrt{14}-140\sqrt{3}*cos(0.5*cos( -\frac{59}{84}))}{184}$
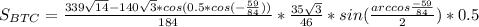
$S_{BTC} =\frac{339\sqrt{14}-140\sqrt{3}*cos(0.5*cos( -\frac{59}{84}))}{184}* \frac{35\sqrt{3}}{46}*sin(\frac{arccos\frac{-59}{84}}{2})*0.5$
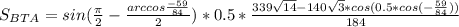
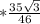
$S_{BTA}=sin(\frac{\pi}{2}-\frac{arccos\frac{-59}{84}}{2})*0.5*\frac{339\sqrt{14}-140\sqrt{3}*cos(0.5*cos( -\frac{59}{84}))}{184}$ $*\frac{35\sqrt{3}}{46}$
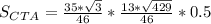
$S_{CTA}=\frac{35*\sqrt{3}}{46}*\frac{13*\sqrt{429}}{46}*0.5$
суммируя получим
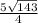
$\frac{5\sqrt{143}}{4}$
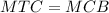
что верно найдя площадь самого треугольник к примеру по формуле Герона является верным ,значит предположение было верным MTC=MCB

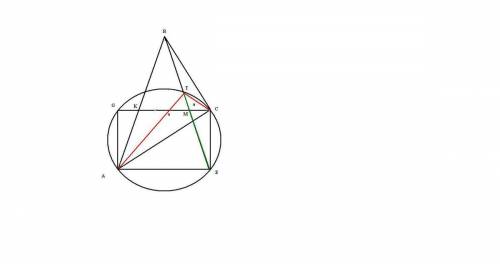
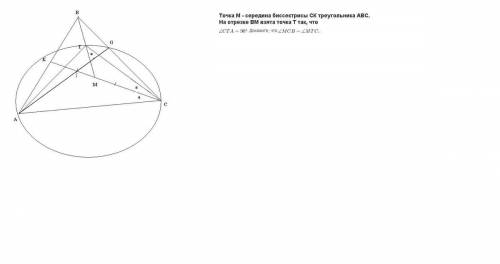
Точка м - середина биссектрисы ск треугольника abс. на отрезке bm взята точка t так, что . докажите,

4,5(44 оценок)

Ответ:

artemykas

04.03.2021

ВС и AD - основания трапеции. Провести дополнительно радиусы окружности OC и OD. А также прямую OM перпендикулярную ВС и AD, которая делит основания пополам. Провести прямую BE перпендикулярную AD. EN=BM=BC/2=1,5. AE=AN-EN=AD/2-EN=1. BE=Корень кв. из (AB^2 - AE^2) = Корень кв. из 3. OD^2=ND^2+ON^2. OC^2=OM^2+MC^2. OM=ON+MN = ON+Корень кв. из 3. OD^2=OC^2. ND=2,5. MC=1,5. ND^2+ON^2 = OC^2+MC^2. 2,5^2 + ON^2 = (ON^2 + Корень кв. из 3)^2 + 1,5^2. Решая уравнение, получим ON^2 = 1/12. Отсюда OD^2 = 19/3. Площадь круга S = Пи * OD^2 = 3 * 19/3 = 19.

4,7(76 оценок)

Это интересно:

Кулинария-и-гостеприимство

23.06.2020

Как заварить Кунг фу чай - лучший способ насладиться вкусом восточного чая...

Кулинария-и-гостеприимство

02.02.2020

Как сделать красивые и вкусные французские макароны с миндалем...

Здоровье

04.01.2023

Контроль гнева: как управлять своими эмоциями...

Семейная-жизнь