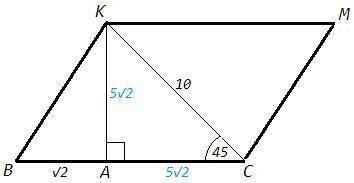
3) Треугольник KAC с углами 45, 90 - стороны относятся 1:1:√2
KA=AC=KC/√2 =10/√2 =5√2
KA - высота, (BA+AC) - основание
S(BKMC)= KA*(BA+AC) =5√2(√2+5√2) =60 (м^2)
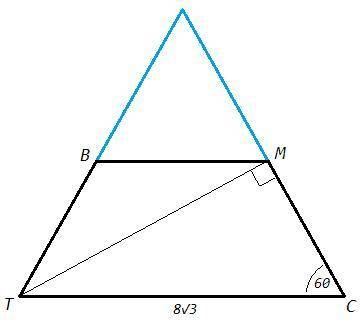
5) Сумма углов при боковой стороне трапеции равна 180 (односторонние углы при параллельных). Угол при основании равен 180-120=60.
Достроим трапецию до треугольника. Так как трапеция равнобедренная и углы при её основании равны 60, получим равносторонний треугольник. Площадь равностороннего треугольника равна a^2 √3/4.
TM - высота в равностороннем треугольнике, следовательно и медиана. Тогда M - середина стороны, BM - средняя линия (параллельна основанию, соединяет середину стороны с точкой на другой стороне). Средняя линия отсекает 1/4 площади, таким образом площадь трапеции равна 3/4 площади треугольника.
S(TBMC)= (8√3)^2 √3/4 *3/4 =36√3 (дм^2)
Площадь трапеции равна (а+b)/2*H.
Рассмотрим треугольник ВKP и треугольник ВСP они равны по трём сторонам (ВС=KP по условию, сторона BP-общая , ВК=СР, тк.точки соединяющие равные отрезки ВС и КР лежат на параллельных прямых ВС и АД). Отсюда имеем: площадь треугольника ВСР =2.
Рассмотрим параллелограмм КВСР (это параллелограмм, т.к стороны равны и попарно параллельны) его площадь равна 2+2=4, по формуле площади параллелограмма находим S=КР*СН (СН- высота параллелограмма опущенная на сторону КР, она же высота трапеции АВСД). Подставим известные значения 4=Х*СН
СН=4/X.
Подставим значение высоты в формулу площади трапеции
S=(X+3*X)/2*4/X=8
Площадь трапеции равна 8