S = 64 см²
Объяснение:
r = 4 см
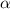= 30
S - ?
=============
Должно выполняться условие, что суммы противоположных сторон четырехугольника равны - только тогда получиться вписать в него окружность.
Распишем это условие: 
⇔ 
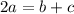. где a - боковые стороны, b и c - основы.
Сделаем вывод, что трапеция являеться равнобедренной.
Формула для нахождения площади через среднюю линию и высоту трапеции: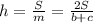 
⇔ 
, где S - площадь трапеции, m - средняя линия трапеции, h - ее высота. 
, b и c - основы трапеции.
Зная радиус вписаной окружности, мы знаем высоту трапеции: 
⇔ 
.
Соответственно, из прямоугольного треугольника ADH1 найдём боковую сторону трапеции с соотношений: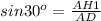 
⇒ 
см - боковая сторона трапеции.
Если 
, то зная а = 8, можем найти среднюю линию, а соответственно и площадь.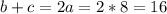 
см.
Просто подставляем в формулу площади: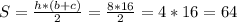 
см².
(а-b)(a+b)=a²-b²
(b³-b²)(b³+b²)=(b³)²–(b²)²=b⁶-b⁴.
(a+b)(a²-ab+b²)=a³+b³
(1+b²)(1²-1*b²+(b²)²)=1³+(b²)³=1+b⁶
Итак,
(b³— b²) (b³ + b²) - (1 + b²) (1 — b² +b⁴) = b⁶–b⁴–(1–b⁶) = b⁶-b⁴–1+b⁶ = 2b⁶–b⁴+1.
2*(0,1)⁶–0,1⁴+1 = 0,000002–0,0001+1 = 0,999902.